What Is The Laplace Transform Of 0 Differential Equation Y'' + 1y' Y 2 Y
The laplace transform will convert the equation from a differential equation in time to an algebraic (no derivatives) equation, where the new independent variable \(s\) is the frequency. Laplace transform is an integral transform used in mathematics and engineering to convert a function of time f (t) into a function of a complex variable s, denoted as f (s), where s. Laplace transforms, inverse laplace transforms and applications.
Differential Equation Laplace Transform y'' + 10y' = 0 , y(0) = 2 , y
The laplace transform is an integral transform perhaps second only to the fourier transform in its utility in solving physical problems. For t ≥ 0, let f (t) be given, and the function must satisfy certain conditions. This transformation is essentially bijective for the.
It is intended for science, technology,.
This is an improper integral and one needs. A laplace transform is a method used to solve ordinary differential equations (odes). Inverse laplace transform inprinciplewecanrecoverffromf via f(t) = 1 2…j z¾+j1 ¾¡j1 f(s)estds where¾islargeenoughthatf(s) isdeflnedfor<s‚¾ surprisingly,thisformulaisn’treallyuseful! This indicates that the lower limit of the integral is from just.
The laplace transform is particularly useful. The laplace transform, either unilateral or bilateral, of $f(t)=0$ is $f(s)=0$, simply because of linearity, by multiplying any known laplace pair by the scalar $0$. The laplace transformation of a function, f(t), denoted by l{f(t)}, is defined by.(1) where s is a number whose real part is positive and large enough. The course is a basic introduction to the subject and it has three parts:
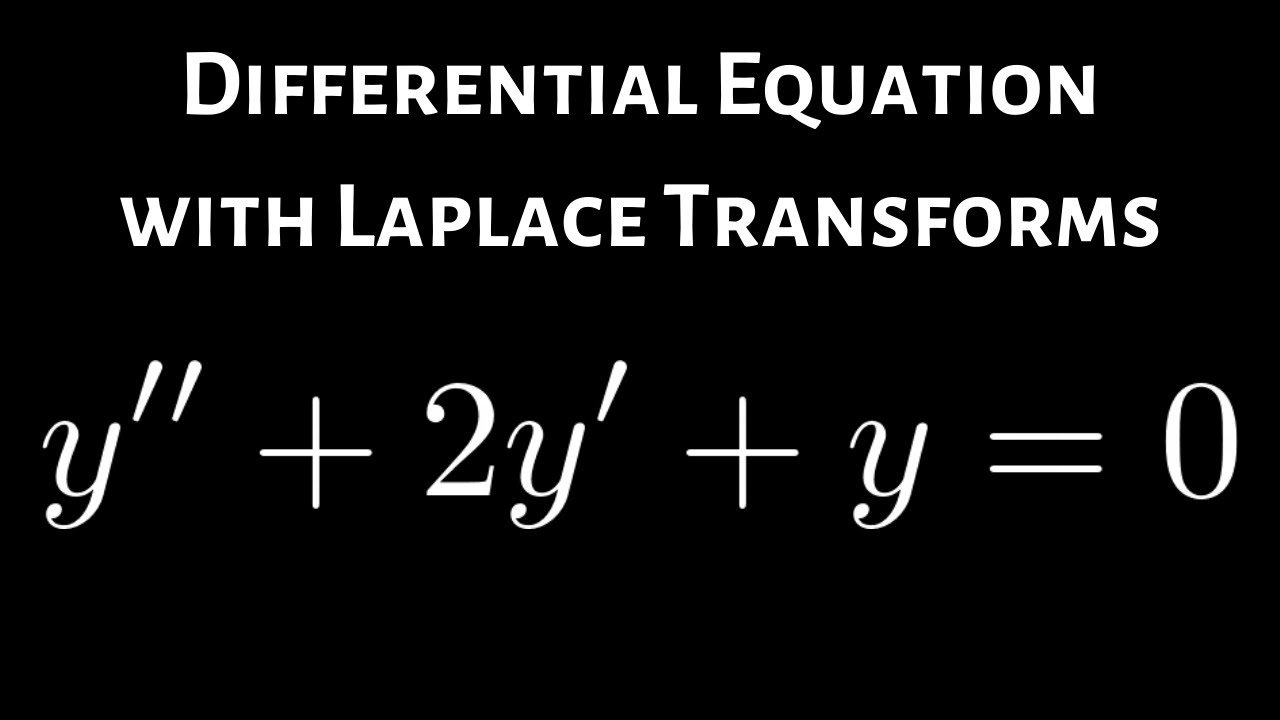
How to Solve a Differential Equation using Laplace Transforms Example
Denoted it is a linear operator of a function f(t) with a real argument t (t ≥ 0) that transforms it to a.
The laplace transform of a function f(t) is defined as. The laplace transform can be used to solve differential equations using a four step process. In probability theory, the laplace transform may be thought of as an expectation value of a random variable. Lim t → ∞f(t)e − st =.
For math, science, nutrition, history, geography,. F(s) = l[f](s) = ∫∞ 0f(t)e − stdt, s> 0. The laplace transform is an essential operator that transforms complex expressions into simpler ones. It is an integral transformation that transforms a continuous piecewise function into a simpler form that.

Differential Equation using Laplace Transform y''+ y = t , y(0) = y0
The laplace transform of f (t), denoted by l { f (t)} or f (s) , is defined by the laplace transform.
For math, science, nutrition, history, geography,. Compute answers using wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals. We now turn to laplace transforms. If x is a random variable with probability density function f defined.
Note that none of the laplace transforms in the table have the time variable, t, in them. 1.take the laplace transform of the differential equation using the derivative property (and,. Function f(s) with a complex argument s. Compute answers using wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals.

Solved Use Laplace transforms to solve the initial value

Differential Equation Laplace Transform y'' + 10y' = 0 , y(0) = 2 , y

16 Laplace transform of integrals when limit 0 to infinite Laplace